Área Lateral de uma pirâmide
Às vezes podemos construir fórmulas para obter as áreas das superfícies que envolvem um determinado sólido. Tal processo é conhecido como a planificação desse sólido. Isto pode ser realizado se tomarmos o sólido de forma que a sua superfície externa seja feita de papelão ou algum outro material.
No caso da pirâmide, a idéia é tomar uma tesoura e cortar (o papelão d)a pirâmide exatamente sobre as arestas, depois reunimos as regiões obtidas num plano que pode ser o plano de uma mesa.

As regiões planas obtidas são congruentes às faces laterais e também à base da pirâmide.
Se considerarmos uma pirâmide regular cuja base tem n lados e indicarmos por A(face) a área de uma face lateral da pirâmide, então a soma das áreas das faces laterais recebe o nome de área lateral da pirâmide e pode ser obtida por:
A(lateral) = n A(face)
Exemplo: Seja a pirâmide quadrangular regular que está planificada na figura acima, cuja aresta da base mede 6cm e cujo apótema mede 4cm.
Como A(lateral)=n.A(face) e como a pirâmide é quadrangular temos n=4 triângulos isósceles, a área da face lateral é igual à área de um dos triângulos, assim:
| A(face) = b h/2 = 6.4/2 = 12 A(lateral) = 4.12 = 48 cm² |  |
|---|
 Exemplo: A aresta da base de uma pirâmide hexagonal regular mede 8 cm e a altura 10 cm. Calcular a área lateral.
Exemplo: A aresta da base de uma pirâmide hexagonal regular mede 8 cm e a altura 10 cm. Calcular a área lateral.Tomaremos a aresta com a=8 cm e a altura com h=10 cm. Primeiro vamos calcular a medida do apótema da face lateral da pirâmide hexagonal. Calcularemos o raio r da base.
Como a base é um hexágono regular temos que r=(a/2)R[3], assim r=8R[3]/2=4R[3] e pela relação de Pitágoras, segue que (ap)²=r²+h², logo:
(ap)²= (4R[3])²+10² = 48+100 = 148 = 4·37 = 2R[37]
A área da face e a área lateral, são dadas por:
A(face) = 8.2[37]/2 = 8.R[37]
A(lateral) = n.A(face) = 6.8.R[37] = 48.R[37]
A(lateral) = n.A(face) = 6.8.R[37] = 48.R[37]
Área total de uma Pirâmide
A área total de uma pirâmide é a soma da área da base com a área lateral, isto é:
A(total) = A(lateral) + A(base)
Exemplo: As faces laterais de uma pirâmide quadrangular regular formam ângulos de 60 graus com a base e têm as arestas da base medindo 18 cm. Qual é a área total?
Já vimos que A(lateral)=n.A(face) e como cos(60º)=(lado/2)/a, então 1/2=9/a donde segue que a=18, assim:
A(face) = b.h/2 = (18.18)/2 = 162
A(lateral) = 4.162 = 648
A(base) = 18² = 324
A(lateral) = 4.162 = 648
A(base) = 18² = 324
Concluímos que:
A(total) = A(lateral) + A(base) = 648+324 = 970
 Exemplo: Um grupo de escoteiros quer obter a área total de suas barracas, as quais têm forma piramidal quadrangular. Para isso, eles usam medidas escoteiras. Cada dois passos de um escoteiro mede 1 metro. A barraca tem 4 passos escoteiros de lado da base e 2 passos de apótema. Calcular a área da base, área lateral e a área total.
Exemplo: Um grupo de escoteiros quer obter a área total de suas barracas, as quais têm forma piramidal quadrangular. Para isso, eles usam medidas escoteiras. Cada dois passos de um escoteiro mede 1 metro. A barraca tem 4 passos escoteiros de lado da base e 2 passos de apótema. Calcular a área da base, área lateral e a área total.A(base) = 2.2 = 4 m²
A(lateral) = 4.2.1 = 8 m³
A(lateral) = 4.2.1 = 8 m³
Logo, a área total da barraca é
A(total) = A(lateral) + A(base) = 8+4 = 12 m²
Volume de uma Pirâmide
O volume de uma pirâmide pode ser obtido como um terço do produto da área da base pela altura da pirâmide, isto é:
Volume = (1/3) A(base) h
 Exemplo: Juliana tem um perfume contido em um frasco com a forma de uma pirâmide regular com base quadrada. A curiosa Juliana quer saber o volume de perfume que o frasco contém. Para isso ela usou uma régua e tirou duas informações: a medida da aresta da base de 4cm e a medida da aresta lateral de 6cm.
Exemplo: Juliana tem um perfume contido em um frasco com a forma de uma pirâmide regular com base quadrada. A curiosa Juliana quer saber o volume de perfume que o frasco contém. Para isso ela usou uma régua e tirou duas informações: a medida da aresta da base de 4cm e a medida da aresta lateral de 6cm.Como V(pirâmide)=A(base).h/3, devemos calcular a área da base e a medida da altura. Como a base tem forma quadrada de lado a=4cm, temos que A(base)=a²=4cm.4cm=16 cm².
 A altura h da pirâmide pode ser obtida como a medida de um cateto de um triângulo retângulo cuja hipotenusa é dada pela altura L=6cm da aresta lateral e o outro cateto Q=2×R[2] que é a metade da medida da diagonal do quadrado. Dessa forma h²=L²-Q², se onde segue que h²=36-8=28 e assim temos que h=2R[7] e o volume será dado por V=(1/3).16.2R[7]=(32/3)R[7].
A altura h da pirâmide pode ser obtida como a medida de um cateto de um triângulo retângulo cuja hipotenusa é dada pela altura L=6cm da aresta lateral e o outro cateto Q=2×R[2] que é a metade da medida da diagonal do quadrado. Dessa forma h²=L²-Q², se onde segue que h²=36-8=28 e assim temos que h=2R[7] e o volume será dado por V=(1/3).16.2R[7]=(32/3)R[7].Seção Transversal de uma pirâmide
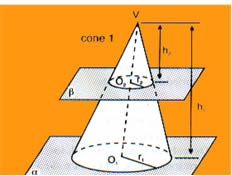
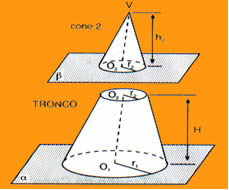
Seção transversal de uma pirâmide é a interseção da pirâmide com um plano paralelo à base da mesma. A seção transversal tem a mesma forma que a base, isto é, as suas arestas correspondentes são proporcionais. A razão entre uma aresta da seção transversal e uma aresta correspondente da base é dita razão de semelhança.
Observações sobre seções transversais:
- Em uma pirâmide qualquer, a seção transversal e a base são regiões poligonais semelhantes. A razão entre a área da seção transversal e a área da base é igual ao quadrado da razão de semelhança.
- Ao seccionar uma pirâmide por um plano paralelo à base, obtemos outra pirâmide menor (acima do plano) semelhante em todos os aspectos à pirâmide original.
- Se duas pirâmides têm a mesma altura e as áreas das bases são iguais, então as seções transversais localizadas à mesma distância do vértice têm áreas iguais.
 | V(seção) | Volume da seção até o vértice (volume da pirâmide menor) |
|---|---|---|
| V(piram) | Volume da pirâmide (maior) | |
| A(seção) | Área da seção transversal (base da pirâmide menor) | |
| A(base) | Área da base da pirâmide (maior) | |
| h | Distância do vértice à seção (altura da pirâmide menor) | |
| H | Altura da pirâmide (maior) |
Assim:
| V(seção) V(base) | = | A(seção) A(piram) | · | h H |
|---|
| A(seção) A(base) | = | h² H² |
|---|
Então:
|
Postado por : Uelder.